2 y d y d x = 4 a. Proof the equation of the chord joining the points t1 and t2 on the parabola y2 = 4ax is y(t1+t2) =.
Equation Of Parabola Y24Ax. ⇒ m2t2−2mt+1=0 ⇒m = 1 t. On differentiating y 2 = 4ax with respect to x, we have:
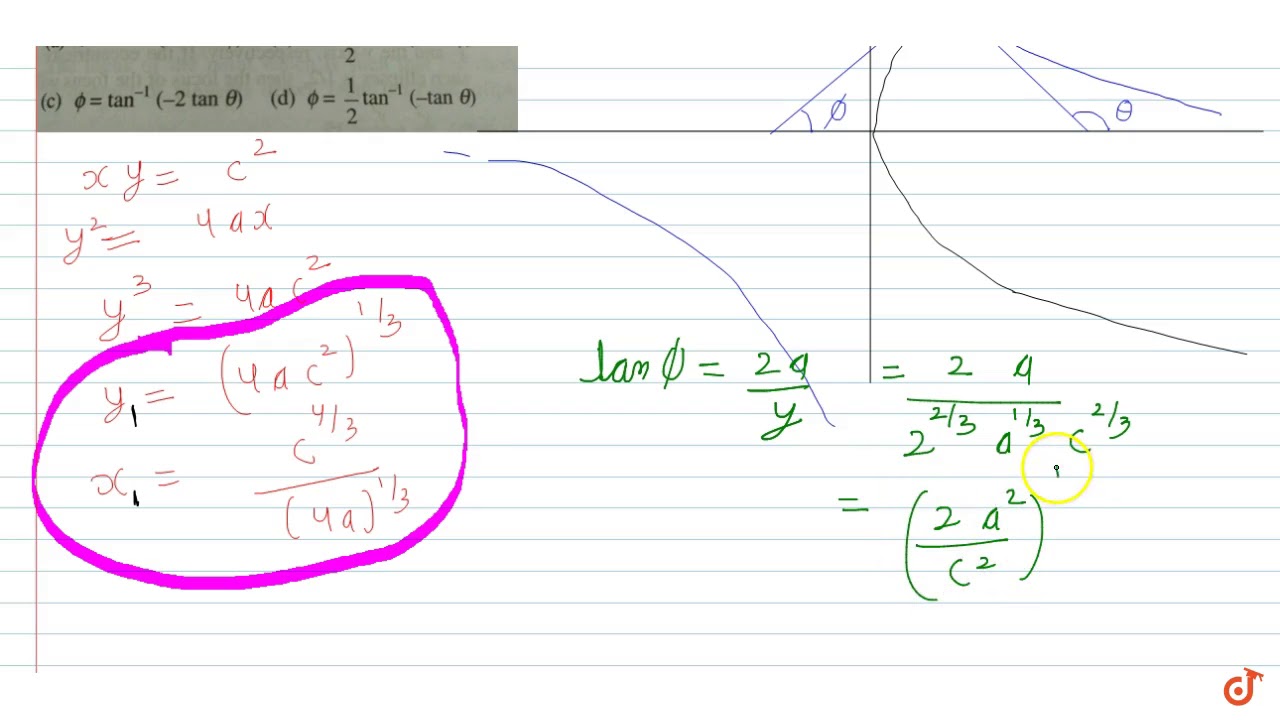
Equation of tangent to parabola y^2 = 4ax YouTube From youtube.com
As a general rule, a parabola is defined as: Which of the following is false? Any point p on the given parabola y² =4ax is (at² , 2at) for every real value of t.
Equation of tangent to parabola y^2 = 4ax YouTube
Misc 8 an equilateral triangle is inscribed in the parabola y2 = 4ax, where one vertex is at the vertex of the parabola. (a) tangent at the vertex is x = 0 Y^(2) =4ax through p (x_(1),y_(1)) then. Let length of equilateral triangle be s hence oa = ob = ab = s here, oc ⊥.
Source: brilliant.org
⇒ d y d x = 2 a y ⇒ a = y 2 d y d x. The length of its latus rectum is 4a and A regular parabola is defined by the equation y2 = 4ax. Y 2 d y d x x. ⇒ equation of normal will be y= −tx+c.
Source: youtube.com
So, y =mx+ a m passes through (at2,2at) ⇒ 2at =mat2+ a m. The sum and product of the slopes of the tangents to the parabola. ⇒ m2t2−2mt+1=0 ⇒m = 1 t. (a) tangent at the vertex is x = 0 (b) directrix of the parabola is x = a (c) focus of the parabola is at (a, 0) (d).
Source: youtube.com
Given equation of parabola is y 2 = 4 a x. ∴ slope of tangent = 1 t. So, y =mx+ a m passes through (at2,2at) ⇒ 2at =mat2+ a m. Each and every point of the parabola must satisfy this relation. Let length of equilateral triangle be s hence oa = ob = ab = s here, oc ⊥.
Source: youtube.com
Example 11find the area of the parabola 𝑦2=4𝑎𝑥 bounded by its latus rectumfor parabola 𝑦2=4 𝑎𝑥latus rectum is line 𝑥=𝑎area required = area olsl’ =2 × area osl = 2 × 0𝑎𝑦 𝑑𝑥𝑦 → parabola equation 𝑦2=4 𝑎𝑥 𝑦=± 4 𝑎𝑥since osl is in 1st quadrant Given equation of parabola is y 2 = 4 a x. The value of.
Source: toppr.com
It passes through the point (h, k) if. We know condition for y=mx+c to be the tangent to y2 =4ax is c = a m. Y 2 d y d x x. The parabola gives a direct relation between x and y. 2 y d y d x = 4 a.
Source: youtube.com
The focus of the parabola is the point (a, 0). Consider the equation of a parabola y 2 + 4ax = 0, where a > 0. To understand some of the parts and features of a parabola, you should know the following terms. (a) tangent at the vertex is x = 0 (b) directrix of the parabola is x =.
Source: brilliant.org
2 y d y d x = 4 a. A regular parabola is defined by the equation y2 = 4ax. The value of x and y are the coordinates in the xy plane. So, y =mx+ a m passes through (at2,2at) ⇒ 2at =mat2+ a m. ⇒ m2t2−2mt+1=0 ⇒m = 1 t.
Source: youtube.com
⇒ y 2 = 2 x y d y d x ⇒ d y d x = y 2 x. We know condition for y=mx+c to be the tangent to y2 =4ax is c = a m. It passes through the point (h, k) if. 2 y d y d x = 4 a. (a) tangent at the vertex is.
Source: teachoo.com
⇒ y 2 = 2 x y d y d x ⇒ d y d x = y 2 x. Consider the equation of a parabola y 2 + 4ax = 0, where a > 0. Equation of parabola is y 2 = 4ax. It passes through the point (h, k) if. We know condition for y=mx+c to be the.
Source: brainly.in
It passes through the point (h, k) if. On differentiating y 2 = 4ax with respect to x, we have: ∴ slope of tangent = 1 t. Any point p on the given parabola y² =4ax is (at² , 2at) for every real value of t. The parabola gives a direct relation between x and y.
Source: teachoo.com
Each and every point of the parabola must satisfy this relation. The sum and product of the slopes of the tangents to the parabola. ⇒ y 2 = 2 x y d y d x ⇒ d y d x = y 2 x. M_(1),m_(2) are the slopes of the tangents of the parabola. ∴ slope of tangent = 1.
Source: doubtnut.com
(a) tangent at the vertex is x = 0 Find the length of the side of the triangle. Substituting the value of a in (i), we get. The length of its latus rectum is 4a and Equation of parabola is y 2 = 4ax.
