As soon as you work a few problems, the process will make sense — we promise. This is the second equation we have been looking for.
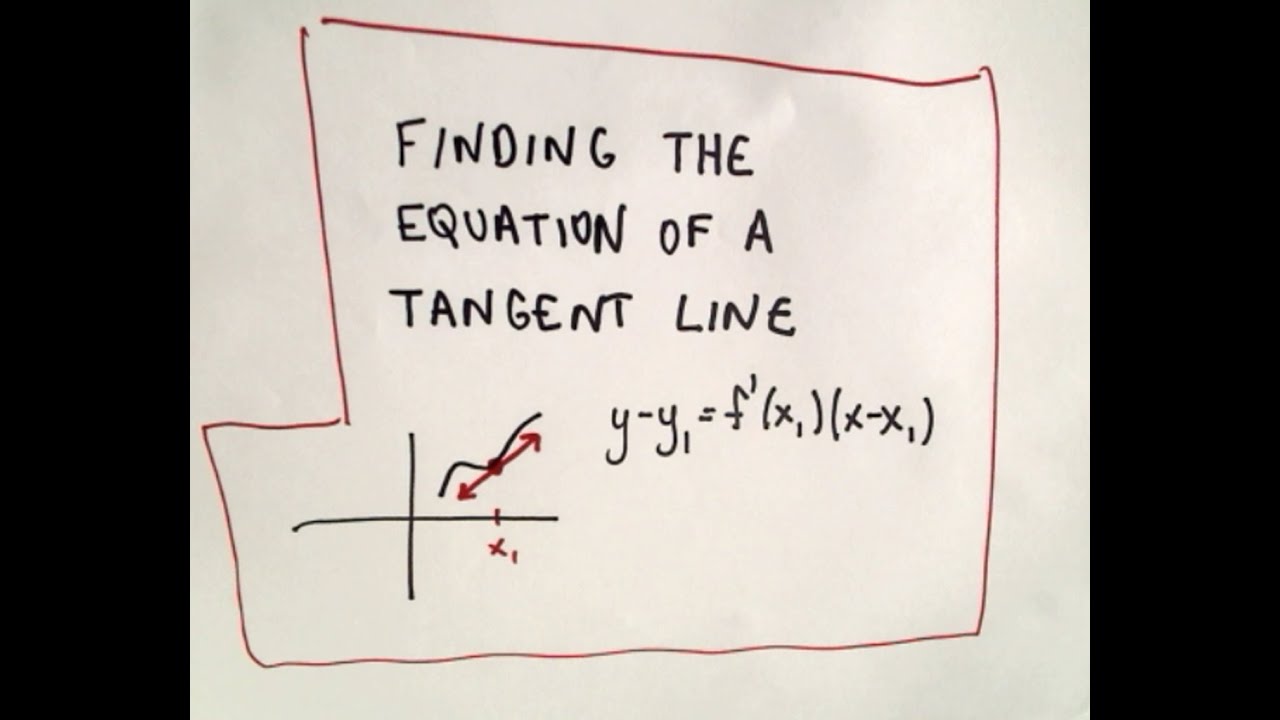
Equation Of A Tangent Line Formula. Then m 2 = 3 b 5 a: In addition, this line assumes that y =y0 y = y 0 ( i.e.
Find the Equation of a Tangent Line Using the Definition From youtube.com
Then m 2 = 3 b 5 a: Thanks to all of you who support me on patreon. Fixed) and a a is the slope of this line.
Find the Equation of a Tangent Line Using the Definition
Equation of the tangent line : You’ll need to find the derivative, and evaluate at the given point. The conversion would look like this: Substitute m q = − 1 2 and q ( 2;
Source: youtube.com
Fixed) and a a is the slope of this line. This article walks through three examples. (2) simplifying this equation, we find 3b b2 = 5a+a2 so 3b+5a = a2 +b2: Substitute m q = − 1 2 and q ( 2; Once we�ve got the slope, we can find the equation of the line.
Source: youtube.com
When a problem asks you to find the equation of the tangent line, you’ll always be asked to evaluate at the point where the tangent line intersects the graph. This article walks through three examples. Both of these attributes match the initial predictions. This is the second equation we have been looking for. When solving for the equation of a.
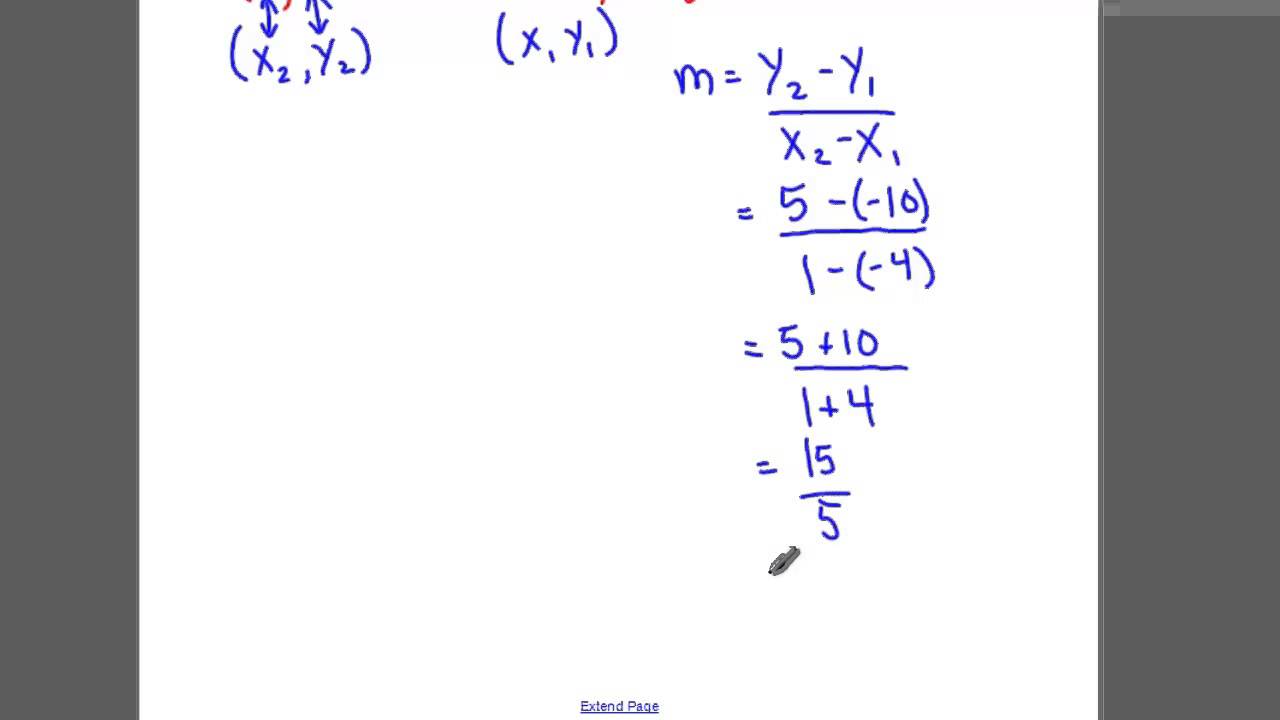Source: youtube.com
This is the second equation we have been looking for. As soon as you work a few problems, the process will make sense — we promise. This structured practice takes you through three examples of finding the equation of the line tangent to a curve at a specific point. Equation of the tangent line at the point (5, 3) is..
Source: teachoo.com
Both of these attributes match the initial predictions. Thanks to all of you who support me on patreon. The tangent of a circle is perpendicular to the radius, therefore we can write: Normal line to a curve. Please consider being a su.
Source: youtube.com
The tangent of a circle is perpendicular to the radius, therefore we can write: We identified it from honorable source. This is the second equation we have been looking for. You’ll need to find the derivative, and evaluate at the given point. Both of these attributes match the initial predictions.
Source: slideshare.net
You’ll need to find the derivative, and evaluate at the given point. Substitute m q = − 1 2 and q ( 2; Y − y 1 = m ( x − x 1) y − 3 = 6 ( x − 1) y = 6 x − 6 + 3 y = 6 x − 3. As the tangent.
Source: youtube.com
Once we�ve got the slope, we can find the equation of the line. The above equation can be written as: Let the slope of the tangent line through (a;b) and (5;3) be m 2. The equation for the tangent line is y=2x+ 3. A curve that is on the line passing through the points coordinates (a, f (a)) and has.
Source: youtube.com
Normal line to a curve. Let the slope of the tangent line through (a;b) and (5;3) be m 2. A curve that is on the line passing through the points coordinates (a, f (a)) and has slope that is equal to f’ (a). Its submitted by dispensation in the best field. You’ll need to find the derivative, and evaluate at.
